 O sistema de numeração egípcio baseava-se em sete números chave: 1, 10,
100, 1.000, 10.000, 100.000 e 1.000.000, um traço vertical representava
1 unidade, um osso de calcanhar invertido representava o número 10, um
laço valia 100 unidades, uma flor de lótus valia 1.000, um dedo dobrado
valia 10.000, um girino representava 100.000 unidades, uma figura
ajoelhada, talvez representando um deus valia 1.000.000.
O sistema de numeração egípcio baseava-se em sete números chave: 1, 10,
100, 1.000, 10.000, 100.000 e 1.000.000, um traço vertical representava
1 unidade, um osso de calcanhar invertido representava o número 10, um
laço valia 100 unidades, uma flor de lótus valia 1.000, um dedo dobrado
valia 10.000, um girino representava 100.000 unidades, uma figura
ajoelhada, talvez representando um deus valia 1.000.000.
Sistema de Numeração Egípcio.
Fonte: Matsubara(2002, p. 42).
Para representar os outros números eram feitas combinações, como por exemplo:

Combinações do Sistema de Numeração Egípcio.
Fonte: Matsubara(2002, p. 43).
Os egípcios não se preocupavam com a ordem dos símbolos, o que para a
atualidade é imprescindível. Esse sistema de numeração servia para
efetuar cálculos que envolviam números inteiros. A técnica era efetuar
todas as operações matemáticas através de uma adição.
Conforme Boyer (1996), o sistema fracionário surgiu no Antigo Egito, às
margens do rio Nilo, por volta do ano de 3.000 a.C. sob o reinado do
faraó Sesóstris. A economia egípcia estava assentada principalmente no
cultivo de terras e para que tal modo de produção ocorresse de uma forma
eficaz, terras cultiváveis eram divididas entre os habitantes.
Anualmente, entre os meses de junho a setembro, as águas do Nilo subiam
muitos metros além de seu leito normal e acabavam por inundar uma vasta
região circundante e trazendo a necessidade de remarcação do terreno não
atingido pela enchente.
Assim, de acordo com o relato que o próprio historiador Heródoto nos
deixou como legado: “se o rio levava qualquer parte do lote de um homem,
o faraó mandava funcionários examinarem e determinarem por medida a
extensão exata da perda”, isto há cerca de 2.300 anos (BOYER,
1996). Tal remarcação era realizada pelos agrimensores do Estado,
conhecidos como estiradores de cordas, estes que utilizavam estas cordas
como unidade de medição no processo de mensuração.
Sesóstris, faraó do Egito, repartiu o solo do Egito entre seus
habitantes, os mais privilegiados. Se o rio levava qualquer parte do
lote de um homem, o rei mandava pessoas para examinar, e determinar por
medida a extensão exata da perda. (BOYER, 1996, p. 6).
Segundo Boyer (1996), o processo de mensuração das terras consistia em
estirar cordas e verificar o número de vezes que a unidade de medida
estava contida no terreno. Havia uma unidade de medida assinada na
própria corda. As pessoas encarregadas de medir esticavam a corda e
verificavam quantas vezes aquela unidade de medida estava contida nos
lados do terreno. Daí, serem conhecidos como estiradores de cordas.
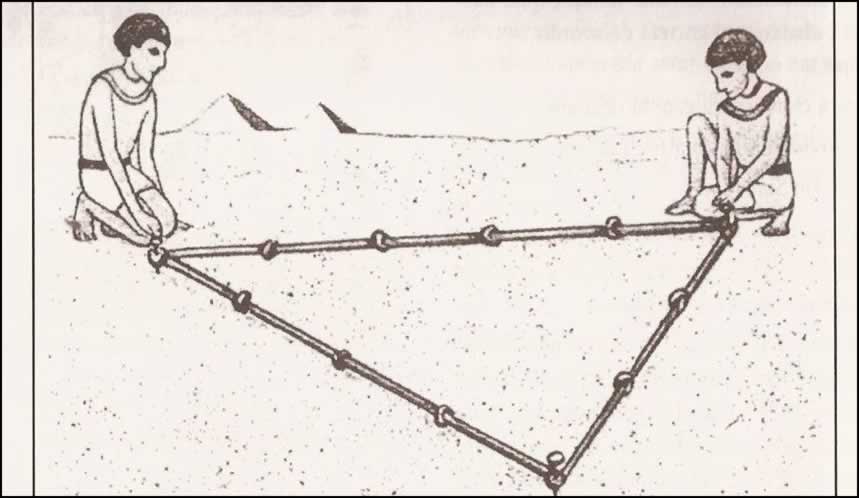
Sistema de cordas.
Fonte: Toledo(1997, p. 19).
No entanto, na maioria das vezes, a medição dificilmente era finalizada
por um número inteiro de vezes em que as cordas eram estiradas. A
resposta encontrada para lidar com a dificuldade imposta por tal
situação consistiu-se na criação dos números fracionários.
A organização do sistema numérico fracionário dos egípcios era baseada
no conceito unitário, de forma que a maioria das frações apresentava o
seu numerador constituído pelo numeral 1 (um) – representado por um
sinal de forma oval e alongada. Tais frações eram denominadas frações
unitárias ou egípcias. Assim: 1/8 correspondia a um símbolo, 1/20
correspondia a outro símbolo. Todavia, duas frações podiam ser apontadas
como exceção a tal regra: 3/4 e 2/3, sendo que o último era contemplado
como fração geral, uma vez que era utilizada como base para diversas
operações matemáticas.
Muitas das frações que não apresentavam o numeral 1 no numerador eram
consideradas o resultado da soma entre as várias frações egípcias
(unitárias). Porém, é importante ressaltar que os sinais de adição e
subtração não eram utilizados nestas operações matemáticas, visto que
ainda não tinham sidos criados.
Os antigos egípcios usavam um sistema de frações baseado em caracteres
distintos, tipo 1/2 era um símbolo, 3/4 era outro, etc., mas tinham
alguma regra geral. Em particular, as frações do tipo 1/2n
(que seriam tipo 1/2,1/4, 1/8, 1/16, 1/32...) tinham símbolos especiais,
surgindo da associação desses símbolos, do 1/2 até o 1/64 é o olho de
Horus. Tem a ver com a série infinita 1/2 + 1/4 + 1/8 + 1/16 + 1/32... =
1. Não se sabe se eles achavam que terminava no 1/64 porque não
conseguiam diferenciar pedaços de coisa menores que isso, mas a idéia
seria que todos juntos formariam a unidade. Cada fração representaria um
sentido, tipo visão, olfato, paladar, tato, audição, e o sexto sentido,
que seria o pensamento. A Figura mostra, no olho de Horus, quais são
os símbolos de cada fração:
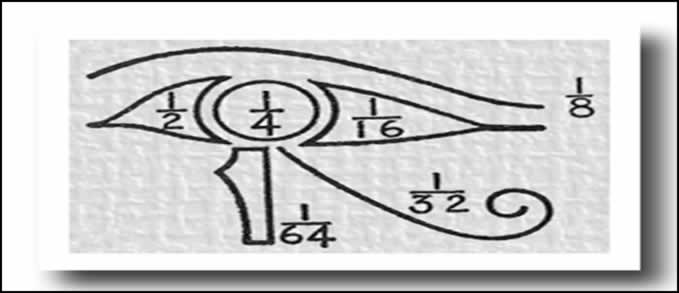
Olho de Horus.
Fonte: Bakos(2005, p. 60).
Onde:
- 1/2 representa o olfato;
- 1/4 representa a visão;
- 1/8 representa o pensamento, que seria a sobrancelha;
- 1/16 representa a audição;
- 1/32 representa o paladar, uma lingüinha bem comprida;
- 1/64 representa o tato, que seriam as duas perninhas em contato com o mundo embaixo.
Conforme Zamboni (2001), é válido apontar a existência de grande
variação, na representação do sistema fracionário segundo a sociedade e a
época histórica. Assim, ao passo que os egípcios utilizavam frações
unitárias na maioria das vezes, os babilônicos e os Sumérios, já por
volta da segunda metade do terceiro milênio, faziam uso de frações cujo
denominador era 60. Era um sistema sexagesimal, onde os números menores
que 60 eram representados por um sistema de base 10 e os números maiores
ou iguais a 60 eram designados pelo mesmo principio com a base 60. Esse
sistema tinha base no princípio proporcional.
É provável que o uso do número 60 pelos babilônios se deve ao fato que é
um número menor do que 100 com maior quantidade de divisores inteiros,
os romanos, por sua vez, usavam constantemente frações com denominador
12. Já os romanos usavam o número 12 por ser um número que embora
pequeno, possui um número expressivo de divisores inteiros.
De acordo com Zamboni (2001), com Grande parte do conhecimento
matemático vigente na Antiguidade foi resgatado pelo achado de inúmeros
registros feitos em papiros, transformando-os em valiosas fontes
históricas. Dois desses importantes documentos encontrados são o Papyrus Rhind e o Papyrus de Moscou,
que tratavam da resolução de diversos problemas matemáticos de caráter
cotidiano (a armazenagem do trigo, o preço do pão, a alimentação do
gado), e outros conteúdos de natureza fracionária.
Acredita-se, que tais documentos apresentavam funções meramente
pedagógicas, sendo destinado ao ensino de funcionários do estado egípcio
e dos escribas. Assim, as frações, desde o tempo dos egípcios auxiliam
de modo significativo ao longo da história o homem no sentido de
facilitar seu processo de compreensão do mundo que o rodeia e de suas
próprias ações.
MATSUBARA, Roberto. Big Mat – Matemática: história, evolução, conscientização. 5. série. 2. Ed. São Paulo: IBEP, 2002.
ZAMBONI, Sílvio. A pesquisa em arte: um paralelo entre arte e ciência. 2. ed. Campinas, SP: Autores Associados, 2001.
BAKOS, Margaret Marchiori (org.). O Imperador na Terra dos Faraós. Revista Nossa História, São Paulo, jan. 2005, n. 15, v. 2.
TOLEDO, M. Didática de matemática: como dois e dois: a construção da Matemática. São Paulo: FTD, 1997.
BOYER, Carl Benjamim. História da matemática. Tradução: Elza F. Gomide. São Paulo: Ed. Edgard, 1996.


Nenhum comentário:
Postar um comentário