Função Quadrática

Ao estudarmos a função afim vimos que sua lei de formação é baseada em um polinômio do primeiro grau na variável x. Analogamente a lei de formação de uma função quadrática é baseada num polinômio do segundo grau na variável x.

Lembre-se que o polinômio ax² + bx + c é um polinômio do segundo grau na variável x.

Vamos analisar o gráfico ao lado e a tabela abaixo que contém alguns pontos deste gráfico:

x	y = -x2 + 10x - 14
2	y = -22 + 10 . 2 - 14 = 2
3	y = -32 + 10 . 3 - 14 = 7
4	y = -42 + 10 . 4 - 14 = 10
5	y = -52 + 10 . 5 - 14 = 11
6	y = -62 + 10 . 6 - 14 = 10
7	y = -72 + 10 . 7 - 14 = 7
8	y = -82 + 10 . 8 - 14 = 2

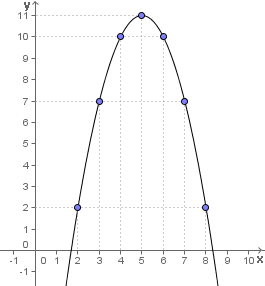
Na tabela temos cada um dos sete pontos destacados no gráfico.
Para traçá-lo primeiro identificamos no plano cartesiano cada um dos pontos sete pontos da tabela e depois fazemos as interligações, traçando linhas curvas de um ponto a outro seguindo a curvatura própria de uma parábola.
Normalmente é mais fácil traçarmos a parábola se a começarmos pelo seu vértice, que neste caso é o ponto (5, 11), visualmente o ponto máximo do gráfico desta parábola.

Ponto de Intersecção da Parábola com o Eixo das Ordenadas

De uma forma geral a parábola sempre intercepta o eixo y no ponto (0, c).
Na função y = -x² + 10x - 14, vista acima, o coeficiente c é igual a -14, portanto a intersecção da parábola do gráfico da função com o eixo das ordenadas ocorre no ponto (0, -14).

Raiz da Função Quadrática

Observe no gráfico anterior que a parábola da função intercepta o eixo das abscissas em dois pontos. Estes pontos são denominados raiz da função ou zero da função.
Uma função quadrática possui de zero a duas raízes reais distintas.
Sendo a função, para encontramos as suas raízes basta igualarmos y a 0 e solucionarmos a equação do segundo grau obtida:










 Estes são os valores de x que levam a y = 0, estes valores são portanto as raízes desta função.

Vértice e Concavidade da Parábola

Podemos observar que no gráfico da função y = -x² + 10x - 14 o seu vértice é o ponto máximo e que a sua concavidade é para baixo.
Agora vamos observar o gráfico da função y = x² + 3x + 1:
Como podemos perceber, esta outra parábola é côncava para cima e o seu vértice é o seu ponto mínimo.


 

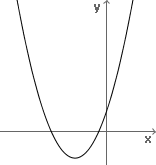
Observando apenas a lei de formação das duas funções, qual o seu palpite para esta divergência entre os dois gráficos?

Vamos identificar os coeficientes destas funções.


Vamos identificar os coeficientes destas funções.
Para a função y = -x² + 10x - 14 temos:

Já para a função y = x² + 3x + 1 temos:


Já tem algum palpite?

 Observe que na primeira função o coeficiente a é negativo, ao passo que na segunda função este mesmo coeficiente é positivo.

 O gráfico da função é côncavo para baixo quando a < 0:

 

 Por outro lado quando a > 0 o gráfico da função tem a sua concavidade voltada para cima:

Coordenadas do Vértice da Parábola

A abscissa do vértice x_v é dada pela fórmula:

Já ordenada do vértice y_v pode ser obtida calculando-se y_v = f(x_v), ou ainda através da fórmula:

Vamos tomar como exemplo novamente a função y = -x² + 10x - 14 e calcularmos as coordenadas do seu vértice para conferirmos com o ponto indicado na tabela inicial.


Seus coeficientes são:

Então para a abscissa do vértice x_v temos:

A ordenada do vértice y_v vamos obter pelas duas formas indicadas. Primeiro utilizando a fórmula, mas para isto antes precisamos calcular o discriminante da equação -x² + 10x - 14 = 0:

Visto que o discriminante é igual a 44, a ordenada do vértice é:

Da outra maneira o cálculo seria:

Portanto o vértice da parábola é o ponto (5, 11) como apontado inicialmente pela tabela.

Valor Mínimo ou Máximo da Função Quadrática

Acima aprendemos a identificar pela lei de formação de uma função se a parábola do seu gráfico tem concavidade para cima ou para baixo e também aprendemos como calcular as coordenadas do vértice desta parábola.
Ficamos sabendo também que as funções polinomiais do 2° grau com coeficiente a < 0 possuem um valor máximo, ao ponto que quando o coeficiente a > 0 possuem um valor mínimo.
Com base nestes conhecimentos podemos calcular qual é o valor máximo ou mínimo de uma função quadrática.

Valor Mínimo e Ponto de Mínimo da Função Quadrática

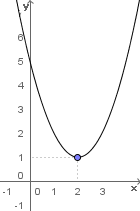
 Vamos analisar o gráfico da função f(x) = x² - 4x + 5:
Os seus coeficientes são:



Esta função é côncava para cima, pois o seu coeficiente a > 0.
O ponto (2, 1) é o vértice da parábola.
2 é a abscissa do vértice, isto é x_v, assim calculado:

1 é a ordenada do vértice, ou seja y_v, que obtemos iniciando pelo cálculo do discriminante:


Conhecendo o discriminante podemos calcular y_v:

Observe que para valores de x menores que a abscissa do vértice, o valor de y vai diminuindo até atingir um valor mínimo que é a ordenada do vértice ou f(x_v).
Como x_v = 2, então f(2) = 1 é o valor mínimo da função f e 2 é o ponto de mínimo da função f.
Para a > 0 o conjunto imagem da função polinomial do 2° grau é:

Valor Máximo e Ponto de Máximo da Função Quadrática

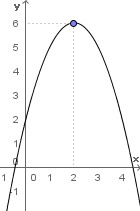
Vamos analisar agora este outro gráfico da função f(x) = -x² + 4x + 2:
Os coeficientes da regra de associação desta função são:



Esta função é côncava para baixo já que o seu coeficiente a < 0.

O ponto (2, 6) é o vértice da parábola.

2 é a abscissa do vértice, ou seja x_v, que calculamos assim:




6 é a ordenada do vértice, isto é y_v, que agora vamos obter calculando f(x_v) diretamente, em vez calcularmos primeiro o discriminante e a partir dele calcularmos y_v, como fizemos no caso do valor mínimo:




Neste caso veja que para valores de x menores que a abscissa do vértice, o valor de y vai aumentando até atingir um valor máximo que é a ordenada do vértice, que como sabemos é f(x_v).
Visto que x_v = 2, então f(2) = 6 é o valor máximo da função f e 2 é o ponto de máximo da função f.
Para a < 0 o conjunto imagem da função quadrática é: