Metodológia para um Bom Ensino sobre Adição de Frações

Devemos vivenciar situações de contextualizações, onde apareçam o conceito, parte-todo, quociente, comparações, equivalências e as operações. Após fazer análise, observações de métodos aplicados no ensino das frações, em várias edições recentes, mesmo que estes métodos não possam ser todos descartáveis, vem a seguinte indagação: “será possível no ensino de frações, desenvolver novas metodologias e aplicações que visem uma melhor compreensão destas?”.

Sim, percebermos que normalmente as crianças têm contato com medidas e valores monetários, nos quais aparecem o décimo e o centésimo, no entanto, o nosso ambiente não coloca para elas, problemas significativos envolvendo números fracionários. Não compramos 3/4 de dúzias de bananas, nem 5/8 de pizza. O vocabulário mais comum em relação ao tema é o meio ou a quarta parte (de certa quantidade), ½ ou ¼ de uma hora. Os materiais concretos podem ter formas geométricas, tiras de papel em tamanhos e cores diferentes, botões, palitos, tampinhas, grãos, fita métrica e balança. 

Há diversas metodologias que podem ser aproveitadas para o ensino de frações. Algumas delas consistem na utilização de materiais concretos, livros didáticos, jogos ou suporte da informática e multimídia, porém todas devem levar em consideração o contexto e o uso cotidiano do aluno. Percebemos que atualmente as escolas, públicas em geral, como também algumas particulares vêm a cada dia exigindo menos dos alunos em relação aos cálculos com frações nas situações do cotidiano.

Outra sugestão com relação às dificuldades metodológicas é a aplicação do conteúdo de frações na qual chagamos a uma conclusão: é que quando falamos em adição de frações com denominadores diferentes, geralmente, recorremos em sala de aula a uma regra tradicional que consiste em determinar o mínimo múltiplo comum (mmc) dos denominadores, sendo que, depois, é necessário fazer algumas operações com o intuito de encontrar frações equivalentes as duas frações dadas com o mesmo denominador. 

Todo esse processo causa enorme desânimo em boa parte dos alunos, já que a operação “divisão” é para muitos um entrave no seu aprendizado. Contudo, graças às nossa busca por novas técnicas, conseguimos encontrar algumas muito interessantes e entre elas destacamos a seguinte, que por ser de melhor compreensão, a operação “multiplicação” torna essa técnica mais agradável e simples. Vejamos a situação abaixo, na qual se pede que se determine a soma das frações que se seguem:

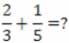
1º) Deve-se encontrar quais frações equivalentes às respectivas frações dadas acima que possuam os mesmos denominadores. Então, tem-se:

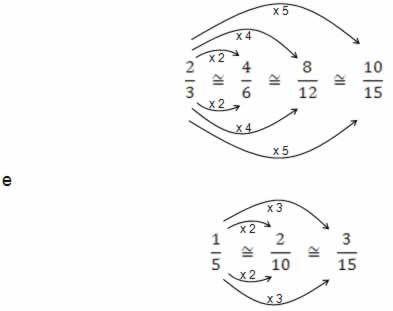
2º) Em seguida, substitui-se as frações dadas pelas suas respectivas equivalências e efetua-se a operação. Assim, tem-se:

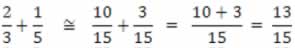
Essa é a nossa pequena, mas importante contribuição, no sentido de facilitar o aprendizado relacionado de forma direta com a adição de frações.

E ainda mais, por meio de situações do cotidiano, onde ocorrem inúmeras situações nas quais se empregam frações, como por exemplo, nas eleições, onde vence o candidato que obtiver ½ (metade) do total de votos mais um no primeiro turno, ou a maioria simples no segundo; em mapas e plantas com o uso de escalas; em razões e proporções empregadas na música, na medicina, na física, na culinária (receitas de tortas, salgados), entre outras aplicações.