Índice
1.
Resumo2. Introdução
3. A Matemática E O Saber
4. O Ensino Dos Números Fracionários No Ensino Fundamental
5. As Frações Na Matemática Hoje
6. Considerações Finais
7. Referências Bibliográficas
1. RESUMO
O presente estudo tem como eixo norteador oferecer possibilidades de
melhor compreensão acerca do tema números fracionários, traçando um
panorama histórico por meio do resgate das questões pertinentes ao
mesmo, dando ênfase à metodologia aplicada no decorrer das séries
iniciais que compõem o Ensino Fundamental. Contribuindo para a
desmistificação do conteúdo, buscando simplificar o estudo das frações,
de maneira a não repetir processos mecânicos de assimilação, e sim,
trazendo para a sala de aula situações que englobem necessidades reais
dos alunos, contextualizando de acordo com a realidade dos mesmos
problemas e situações a serem trabalhadas na busca de soluções,
utilizando as técnicas e os conceitos fracionários que podem ser
trabalhados tanto em sala de aula, como também utilizando pesquisa
extraclasse, ou seja, ligada ao dia-a-dia de cada aluno, devendo as
atividades ser sugeridas pelo próprio professor, usando, com isso, suas
habilidades metodológicas. Por isso, a necessidade de profissionais
preparados e competentes para o ensino-aprendizagem desta disciplina e
deste conhecimento tão antigo, mas que a cada dia se torna ainda mais
necessário.
Palavras-chave: Ensino. Frações. Números fracionários.
ABSTRACT
The present study has as guiding axis to offer possibilities of better
understanding concerning the theme fractional numbers, drawing a
historical panorama through the rescue of the pertinent subjects to the
same, giving emphasis to the applied methodology in elapsing of the
initial series that compose the Fundamental Teaching. Contributing to
the demystification of the content, looking for to simplify the study of
the fractions, in way to not to repeat mechanical processes of
assimilation, but, bringing for the classroom situations that include
the students' real needs, contextualized in agreement with the reality
of the same problems and situations to be worked in the search of
solutions, using the techniques and the fractional concepts that
you/they can be worked so much at classroom, as well as using researches
extra class, in other words, linked to each student's day by day, owing
the activities to be suggested by the own teacher, using, with that,
their methodological abilities. Therefore, the prepared and competent
professionals' need for the teaching-learning of this discipline and of
such old knowledge, but that every day becomes still more necessary.
Keywords: Education. Fractions. Fractional numbers.
2. INTRODUÇÃO
O presente trabalho é resultado de uma pesquisa bibliográfica
realizada com o objetivo de relacionar o ensino das frações no ensino
fundamental com a sua história e mostrar que atividades práticas,
realizadas em sala de aula pelo docente devidamente preparado, podem
facilitar o processo ensino aprendizagem deste conteúdo.
Este trabalho foi realizado através de revisão de literatura, a fim de
propor um referencial teórico-analítico para o estudo proposto, com o
intuito de analisar diferentes definições e utilizar-se de um
embasamento científico.
De acordo com Rúdio (1986), o método da pesquisa científica não é
outra coisa do que a elaboração, consciente e organizada, dos diversos
procedimentos que nos orientam para realizar o ato reflexivo, isto é, a
operação discursiva na nossa mente. Conforme Gil (1999), este tipo de
estudo é desenvolvido por meio de material já elaborado, constituído
principalmente de livros e artigos científicos, sendo elaborado a partir
de autores e referências já consolidadas cientificamente.
O conhecimento dos números fracionários precisa fazer parte da
formação dos docentes para que tenham elementos que lhes permitam
ensinar os alunos de uma melhor forma e com competências, tratando da
história, do conceito teórico até às implicações práticas das frações no
cotidiano. Aqui se faz um estudo a respeito desse tema para que atuais e
futuros educadores observem alguns dos aspectos que envolvem o estudo
das frações e sua aprendizagem por parte dos alunos, partindo do
conhecimento dos obstáculos que se encontram no processo de ensino e
aprendizagem de tais conceitos.
Lidar com os conceitos matemáticos não é uma tarefa muito simples,
ensinar exige mais esforço ainda, pois se exige não somente o
conhecimento do conteúdo que se pretende ensinar como também sobre o
público alvo, o modo como ele aprende. Partiremos então, nesse trabalho,
para um estudo não só sobre as frações (sua história, conceito, modos
de resoluções de problemas), mas sobre como ensiná-las.
O objetivo geral deste trabalho é evidenciar a necessidade de rever a
metodologia aplicada. Mais especificamente, conhecer a história das
frações, compreender a sua importância nas séries iniciais, como também,
promover mudanças que venham facilitar a aprendizagem desse conteúdo.
O primeiro Capítulo fala da importância da Matemática como ciência e
da sua utilização como investigação científica e no dia-a-dia do homem.
Enfatiza seu objeto de estudo e a importância da adequação nas escolas
para proporcionar o ensino-aprendizagem. A formação do professor de
Matemática deve ser seguida passo a passo, de forma que ele saiba
realmente a profissão que está escolhendo e suas possibilidades. Neste
capítulo, também é possível ter conhecimento da utilização dos números
fracionários pelos egípcios e seu sistema de numeração.
No segundo Capítulo é possível ter uma visão, à luz dos Parâmetros
Curriculares Nacionais (PCNs), da utilização dos números fracionários no
Ensino Fundamental. Como é aplicada a definição, os conceitos, os
cálculos e as atividades, como também as falhas do currículo atual em
ralação ao ensino das frações também é visto neste capítulo. Sugestões e
reflexões sobre o número fracionário enceram este capítulo de forma
introdutória ao próximo.
O Capítulo três faz uma narrativa da aplicação dos números fracionários, de acordo como os PCNs, no Ensino Fundamental.
Buscar o conhecimento a respeito desse assunto não só importa porque
ele deve ser ensinado, por conta de estar no currículo escolar, mas
porque faz parte de uma herança cultural que ajudará os alunos a
entenderem o progresso da invenção humana, bem como a resolver as
situações do cotidiano, conforme sua utilização pelos povos egípcios.
3. A MATEMÁTICA E O SABER
3.1 O Ensino da Matemática e sua Importância
A Matemática possui grande valor formativo. É a ciência dos números e
dos cálculos, sendo largamente utilizada na investigação científica para
facilitar a vida do homem e organizar a sociedade civil, uma vez que
possui valor pedagógico e concede incalculáveis oportunidades de
ascensão a quem domine seu método e teoria, despertando o pensamento.
Entretanto, ainda hoje, o ensino matemático é uniformizado, não levando
em consideração as diferenças individuais do educando, frustrando-o e
fazendo com que se achem inferiores e passem a bloquear mentalmente a
aprendizagem matemática.
Conforme Piletti (2003), o ensino visa à aprendizagem e a aprendizagem
é um fenômeno, um processo bastante complexo, existindo muitas teorias a
esse respeito.
O objeto de estudo da educação matemática consiste nas múltiplas
relações e determinações entre ensino, aprendizagem e conhecimento
matemático. Esses objetivos variam de acordo com cada problema ou
questão de pesquisa: um visa à melhoria da qualidade do ensino e da
aprendizagem; o outro é de natureza científica e visa desenvolver a
educação matemática enquanto investigação e produto de conhecimento.
Assim, deve-se pensar num ensino matemático que se desenvolve a partir
de problemas do mundo real em que vive os homens, privilegiando
conhecimentos que podem ser apresentados de maneira adequada para ser
utilizados nas diferentes situações que fazem parte da vida numa
sociedade moderna, como o que ocorreu no Antigo Egito, quando se
utilizou o sistema de cordas.
A escola deve adequar o ensino matemático à realidade de seu alunado,
bem como, deve buscar capacitar o seu corpo docente a respeito da melhor
forma didática de ensinar. Visto que, a mesma tem sido utilizada pelo
indivíduo para resolver os mais variados problemas.
Através da indução, dedução, abstração e analogia. Tomando dos dados
provenientes do estudo da matemática, observa-se que eles podem ser
ferramentas para o desenvolvimento de ações cidadãs. Neste sentido, a
Matemática ocupa grande parte do nosso tempo, indo além do ensino
formal, mas sim, perpassando nossas atividades cotidianas, uma vez que
está profundamente ligada a história do desenvolvimento da sociedade,
desde seus primórdios até os dias atuais. Constitui-se um valioso
instrumento para a análise e interpretação de problemas recorrentes a
investigação e buscando soluções práticas para a resolução de questões
apresentadas ao indivíduo no seu dia-a-dia.
O educador precisa orientar os docentes no sentido de fazê-los
desenvolver um senso crítico, onde os mesmos questionem, levantem
hipóteses e criem soluções, transformando-se em agentes diretos da sua
aprendizagem. O saber matemático deve levar a experimentação,
envolvendo, questionando e levando o aluno a mergulhar num universo
fascinante, onde o processo ensino aprendizagem se desenvolva num
ambiente propício à resolução dos problemas.
Conforme os Parâmetros Curriculares Nacionais do Ensino Fundamental (1a a 4a
série do Ensino Fundamental de 8 anos – 1997), a Matemática, surgida na
Antiguidade por necessidades da vida cotidiana, converteu-se em um
imenso sistema de variadas e extensas disciplinas. Como as demais
ciências, a Matemática reflete as leis sociais e serve de poderoso
instrumento para o conhecimento do mundo e domínio da natureza, como por
exemplo, iniciar o reflorestamento de uma área ou a criação de um
jardim, através de planejamentos que envolvam o cálculo e a resolução de
problemas.
Mesmo com um conhecimento superficial da Matemática, é possível
reconhecer certos traços que a caracterizam: abstração, precisão, rigor
lógico, caráter irrefutável de suas conclusões, bem como o extenso campo
de suas aplicações.
Os resultados matemáticos distinguem-se pela sua precisão e os
raciocínios desenvolvem-se num alto grau de minuciosidade, que os torna
incontestáveis e convincentes. Mas a vitalidade da Matemática deve-se
também ao fato de que, apesar de seu caráter abstrato, seus conceitos e
resultados têm origem no mundo real e encontram muitas aplicações em
outras ciências e em inúmeros aspectos práticos da vida diária: na
indústria, no comércio e na área tecnológica. Por outro lado, ciências
como Física, Química e Astronomia têm na Matemática ferramenta essencial
(BRASIL, 1997, p. 24).
Tomando como base os PCNs (BRASIL, 1997), percebe-se que a Matemática como uma área de conhecimento que
Comporta um amplo campo de relações, regularidades e coerências que
despertam a curiosidade e instigam a capacidade de generalizar,
projetar, prever e abstrair, favorecendo a estruturação do pensamento e o
desenvolvimento do raciocínio lógico (BRASIL, 1997, p. 25).
A Matemática tem um papel essencial no Ensino Fundamental. Os
conhecimentos matemáticos podem ajudar na formação das capacidades
intelectuais, a estruturar o pensamento, a agilizar o raciocínio
dedutivo do aluno, tanto na sua aplicação a problemas, como na vida
cotidiana e nas atividades do mundo do trabalho e, até mesmo no auxílio
da construção do conhecimento em outras áreas curriculares.
Não há como negar que a Matemática faz parte da construção da
cidadania, uma vez que para sobreviver em uma sociedade complexa como a
atual, é necessário ter, cada vez mais, conhecimento. Conforme
os PCNs, para exercer a cidadania é necessário saber calcular, medir,
raciocinar, argumentar, tratar informações estatisticamente
O mundo do trabalho requer pessoas preparadas para utilizar diferentes
tecnologias e linguagens (que vão além da comunicação oral e escrita),
instalando novos ritmos de produção, de assimilação rápida de
informações, resolvendo e propondo problemas em equipe (BRASIL, 1997, p.
30).
É dessa forma que a Matemática tem importante função no Currículo
Nacional do Ensino Básico; fazer com que através de seus conteúdos, o
cidadão faça assimilações rápidas de informações e resolva problemas
cotidianos.
A leitura e a escrita de textos como também a ordenação e
representação fracionária de uso freqüentes têm facilitado a
aprendizagem, como também o reconhecimento de que os números racionais
admitem infinitas (diferentes) representações gráficas e de
regularidades nas escritas numérica tem contribuido para a aprendizagem
de frações na sala de aula.
3.2 O Currículo de Matemática e a Formação do Professor
De acordo com Schubring (1999), a Matemática foi a primeira das
disciplinas escolares a deflagrar um movimento internacional de
reformulação curricular. Esse movimento aconteceu a partir da Alemanha,
no início do século XX, sob a liderança do matemático Félix Klein.
Depois a iniciativa veio das universidades européias em promover
formalmente a formação de professores secundários, contribuindo para o
surgimento de especialistas universitários em ensino de Matemática.
Experimentos realizados por psicólogos americanos e europeus, desde o
início do século XX, sobre o como as crianças aprendiam Matemática
também foram de grande importância para a iniciativa da pesquisa
matemática.
Mas a pesquisa em Matemática teve seu ápice significativo em nível
internacional a partir do “Movimento da Matemática Moderna”, nos anos 50
e 60. Dentre os grupos influentes que surgiram, está o School Mathematics Study Group,
que publicou livros didáticos e disseminou o ideário modernista,
atingindo o Brasil, onde surge a Sociedade Brasileira de Educação
Matemática (SBEM) e os primeiros programas de pós-graduação em Educação
Matemática. Os norte-americanos fundaram os primeiros programas
específicos de mestrado e doutorado em Educação Matemática. De acordo
com Kilpatrick (1992), até o final dos anos 80, já haviam sido
realizados mais de cinco mil estudos na área, a maioria nos Estados
Unidos.
Alguns fatores provocam mudanças curriculares no ensino da Matemática
como: as pressões sociais, econômicas e políticas em relação a formação
de novos profissionais e a pressão dos especialista e acadêmicos em
querer transpor para sala de aula os resultados de suas pesquisas sobre o
ensino da Matemática. Outro fator que pode acarretar mudanças no
currículo é atribuída aos próprios professores, que através de pesquisas
e iniciativas, produzem inovações.
A formação profissional do professor é realizada nos cursos de
Habilitação ao Magistério em níveis de 2º grau e superior. Compõe-se de
um conjunto de disciplinas coordenadas e articuladas entre si, cujos
objetivos e conteúdos devem confluir para uma unidade
teórico-metodológica do curso. A formação profissional é um processo
pedagógico, intencional e organizado, de preparação teórico-científica e
técnica do professor para dirigir competentemente o processo de ensino
(LIBÂNEO, 1994, p. 27).
Vale salientar que um curso de formação inicial de professores de
Matemática deve ser diferente de um curso de Matemática que tem a
intenção de formar matemáticos voltados para a investigação, à pesquisa.
Essa formação deve preparar profissionais para o exercício da profissão
de professor. Contudo, o futuro professor, tem uma formação pessoal,
social e cultural que muitas vezes é ignorada. Formação esta que o pode
favorecer no desenvolvimento da capacidade de reflexão, autonomia,
cooperação e participação, interiorização de valores, capacidade de
percepção de princípios, de relação interpessoal, dentre outros. A
formação científica e tecnológica, técnica ou artística na respectiva
especialidade é imprescindível; sem o domínio do conteúdo e competência,
o professor não pode exercer de modo adequado suas funções.
A formação no domínio educacional deve estar presente na formação do
discente em qualquer disciplina, inclusive Matemática. Um professor está
envolvido com a herança da pedagogia, com os tributos das ciências da
educação, da reflexão sobre os problemas educacionais do mundo, das
problemáticas e dos contributos da investigação realizada pela didática e
pelas áreas das ciências da educação, torna-se cada vez mais um
educador. Isso pode ser verificando quando o aluno consegue fazer um
paralelo entre o que aprende em sala de aula e a sua realidade do
dia-a-dia. Quando o mesmo reflete e analisa antes de resolver qualquer
situação, ou seja, qualquer problema.
O professor de Matemática tem de ser capaz de construir soluções para
diversas situações da sua vida profissional, deve ser capaz de lidar com
situações concretas e não apenas conhecer teorias e resultados de
investigações. O professor é um profissional que tem a capacidade de
identificar os problemas que surgem na sua atividade, construindo,
sempre que possível, com soluções adequadas. Essas competências devem
estar presentes na formação inicial do professor, mas principalmente ao
longo de sua carreira profissional.
Todavia, se a formação não prepara o professor para se inserir na
realidade educacional que existe hoje, com seus alunos e suas culturas,
seus problemas estruturais e financeiros, teremos profissionais
deslocados, inaptos e descontentes, podendo até mesmo abandonar a
profissão antes mesmo de começar a exercê-la.
O estágio pedagógico que os alunos do Curso de Licenciatura em
Matemática realizam visa o desenvolvimento de competências dos
estagiários no âmbito da prática e na participação ativa da escola, numa
perspectiva de aperfeiçoamento profissional permanente no que diz
respeito ao domínio científico, didático, pedagógico e relacional. Na
verdade, é uma forma de vivenciar a profissão de uma forma mais
abrangente, onde você esta sendo avaliado e ao mesmo tempo se avalia. Um
estagiário tem a possibilidade de verificar as metodologias aplicadas
em diferentes anos e de diferentes formas, contribuindo e enriquecendo
seu processo de formação.
Conforme Lampert e Ball (1998), mais importante que saber as
competências que devem ter os novos professores é saber como é que eles
as devem adquirir. No ensino, como em outros campos de conhecimento, os
profissionais precisam saber como construir novo conhecimento.
3.3 Os Números Fracionários na História da Matemática
Não é possível datar o exato momento do aparecimento da Matemática,
mas ela surgiu como ciência, a partir dos séculos VI e V a.C. na Grécia,
dando sentido aos símbolos, designando números, segmentos de retas,
entes geométricos, entre outros.
No século VI a.C., por exemplo, num momento em que as demais cidades
gregas, de uma forma ou de outra, orientavam-se para a democracia,
Esparta mantinha-se aristocrática e sua educação visava exclusivamente à
formação de soldados. Nesse mesmo período, a organização social de
Atenas começa a ser modificada e “a uma data infelizmente difícil de se
precisar [...] perdeu a educação seu caráter essencialmente militar”
(MARROU, 1975, p. 66).
É justamente nesse momento que a educação grega, e em especial,
Atenas, começou a valorizar o ensino de modo geral, ou seja, abrangendo a
leitura e a escrita para a formação dos filhos dos nobres. Só após um
século é que foi possível tornar o ensino da Matemática também
importante nessa formação.
Conforme Marrou (1975), porvolta do ano 4000 a.C., algumas comunidades
primitivas aprenderam a usar ferramentas e armas de bronze. As aldeias
que estavam situadas às margens de rios transformaram-se em cidade,
tornando a vida cada vez mais complexa, devido ao surgimento
principalmente de novas atividades e do desenvolvimento do comércio e da
necessidade de produzir mais alimentos para suprir suas necessidades e
às necessidades dos compradores. Outras atividades também tiveram que
ser desenvolvidas como o artesanato, o sacerdócio e a administração.
Os grandes progressos que marcaram o final da Pré-história tornaram-se
bem evidentes no Egito, uma vez, que havia a necessidade de efetuar
cálculos rápidos e precisos e, para isto, era necessário representar a
quantidade de objetos de uma coleção. Para isto, passou-se a utilizar,
desenhos, que a posterior, se chamaram símbolos. Esse foi um passo muito
importante para o desenvolvimento da Matemática. Na Pré-história, o
homem juntava 3 bastões com 5 bastões para obter 8 bastões. Hoje, se
utiliza os símbolos para representar tal operação: 3 + 5 = 8.
Ainda de acordo com Marrou (1975), a cultura egípcia desenvolveu-se no
noroeste da África, no vale do Nilo, desde aproximadamente o ano 3200
a.C. até os primeiros séculos da era cristã. Esse vale manteve-se em
isolamento, protegido naturalmente de invasões estrangeiras devido a sua
geografia, governando pacificamente e quase ininterruptamente por uma
sucessão de dinastias. Nessa cultura egípcia foram desenvolvidas três
formas de escrita, sendo a mais antiga e utilizada pelos sacerdotes em
monumentos e tumbas, a hieroglífica, dando origem à chamada hierática da
qual surgiu mais tarde a escrita demótica que se tornou de uso geral.
Segundo Marrou (1975), no período da campanha de Napoleão no Egito
(1799), encontraram, durante escavação no solo perto do braço Roseta do
delta do Nilo, um fragmento basáltico polido que iria propiciar a
decifração da escrita egípcia. Ficou conhecida como Pedra de Roseta e
contém inscrições com uma mensagem repetida em hieroglíficos, em
caracteres demóticos e em grego. Tendo o grego como chave, foi possível
decifrar a escrita egípcia. Para fazer os projetos de construção das
pirâmides e dos templos, o número concreto não era nada prático, como
também não ajudava muito na resolução dos difíceis problemas surgidos
das necessidades do desenvolvimento da indústria e do comércio. Na
construção das pirâmides foi possível notar uma perícia profunda na arte
de engenharia.
Dois papiros são as fontes principais de informação referentes à
Matemática antiga no Egito: o papiro Golonishev, ou Moscou datado de
1850 a.C., consiste numa tira de 5,5 m de comprimento por 8 cm de
largura com 25 problemas e o papiro Rhind (ou Ahmes) de 1650 a.C., com
5,5 m de comprimento e 32 cm de largura, considerado um antigo manual de
matemática, contendo 85 problemas resolvidos que, em sua maioria,
envolve assuntos do dia-a-dia, descrevendo métodos de multiplicação e
divisão dos egípcios, o uso de frações unitárias, dentre outros. Foi
comprado, em 1.858, por um antiquário escocês chamado Henry Rhind e
atualmente encontrando-se no British Museum, de Londres.
De acordo com Boyer (1974), Vinte e seis dos 110 problemas dos papiros
Moscou e Rhind são geométricos. Muitos deles decorrem de fórmulas de
mensuração necessária para cálculo de áreas de terras e volumes de
grãos. A área de um círculo é tomada igual a de um quadrado de lado
igual a 8/9 do diâmetro, o equivale a notação atual a tomar uma
aproximação para π igual a 3,16.
Surgiram muitos problemas clássicos, onde se sentia a necessidade de
expressar um pedaço de alguma coisa através de um número. Dessa
necessidade de resolver esses problemas, principalmente se estavam
relacionados ao rio Nilo, os egípcios desenvolveram o número fracionário
e para representá-lo, a fração.
3.4 O Sistema de Numeração Egípcia
O sistema de numeração egípcia baseava-se em sete números chave: 1,
10, 100, 1.000, 10.000, 100.000 e 1.000.000, um traço vertical
representava 1 unidade, um osso de calcanhar invertido representava o
número 10, um laço valia 100 unidades, uma flor de lótus valia 1.000, um
dedo dobrado valia 10.000, um girino representava 100.000 unidades, uma
figura ajoelhada, talvez representando um deus valia 1.000.000.

Figura 1:Sistema de Numeração Egípcia.
Fonte: Matsubara(2002, p. 42).
Para representar os outros números eram feitas combinações, como por exemplo:
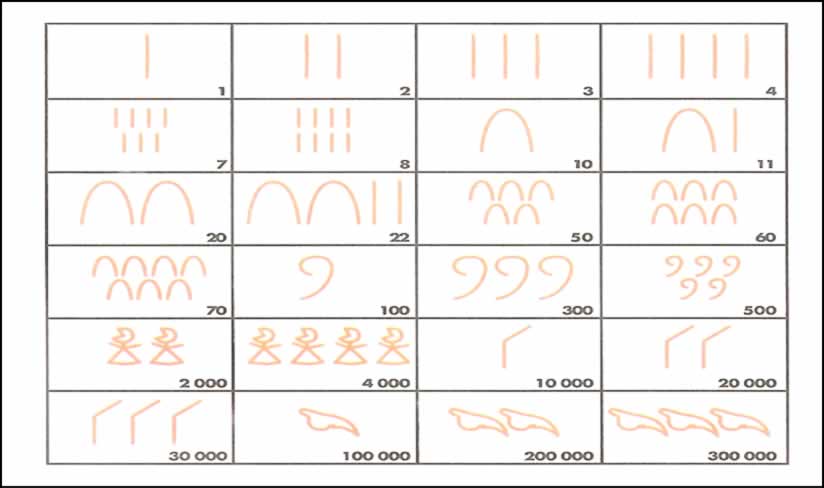
Figura 2:Combinações do Sistema de Numeração Egípcia.
Fonte: Matsubara(2002, p. 43).
Os egípcios não se preocupavam com a ordem dos símbolos, o que para a
atualidade é imprescindível. Esse sistema de numeração servia para
efetuar cálculos que envolviam números inteiros. A técnica era efetuar
todas as operações matemáticas através de uma adição.
Conforme Boyer (1996), o sistema fracionário surgiu no Antigo Egito,
às margens do rio Nilo, por volta do ano de 3.000 a.C. sob o reinado do
faraó Sesóstris. A economia egípcia estava assentada principalmente no
cultivo de terras e para que tal modo de produção ocorresse de uma forma
eficaz, terras cultiváveis eram divididas entre os habitantes.
Anualmente, entre os meses de junho a setembro, as águas do Nilo subiam
muitos metros além de seu leito normal e acabavam por inundar uma vasta
região circundante e trazendo a necessidade de remarcação do terreno não
atingido pela enchente.
Assim, de acordo com o relato que o próprio historiador Heródoto nos
deixou como legado: “se o rio levava qualquer parte do lote de um homem,
o faraó mandava funcionários examinarem e determinarem por medida a
extensão exata da perda”, isto há cerca de 2.300 anos (BOYER,
1996). Tal remarcação era realizada pelos agrimensores do Estado,
conhecidos como estiradores de cordas, estes que utilizavam estas cordas
como unidade de medição no processo de mensuração.
Sesóstris, faraó do Egito, repartiu o solo do Egito entre seus
habitantes, os mais privilegiados. Se o rio levava qualquer parte do
lote de um homem, o rei mandava pessoas para examinar, e determinar por
medida a extensão exata da perda. (BOYER, 1996, p. 6).
Segundo Boyer (1996), o processo de mensuração das terras consistia em
estirar cordas e verificar o número de vezes que a unidade de medida
estava contida no terreno. Havia uma unidade de medida assinada na
própria corda. As pessoas encarregadas de medir esticavam a corda e
verificavam quantas vezes aquela unidade de medida estava contida nos
lados do terreno. Daí, serem conhecidos como estiradores de cordas.
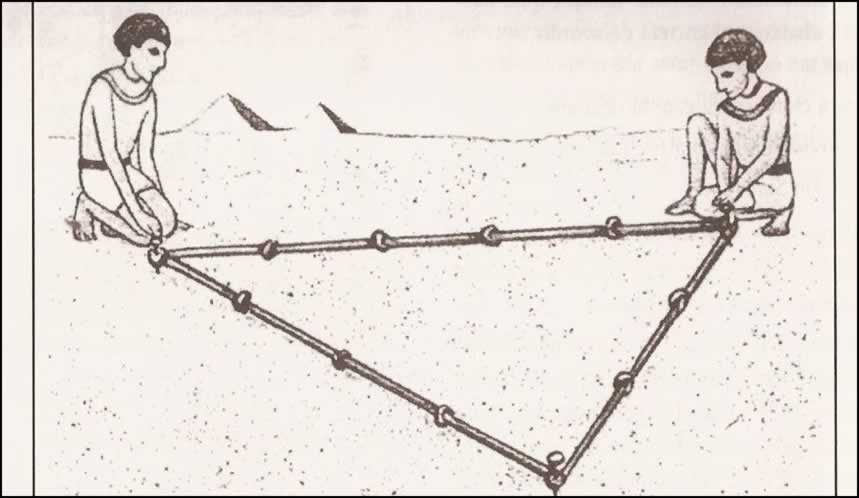
Figura 3:Sistema de cordas.
Fonte: Toledo(1997, p. 19).
No entanto, na maioria das vezes, a medição dificilmente era
finalizada por um número inteiro de vezes em que as cordas eram
estiradas. A resposta encontrada para lidar com a dificuldade imposta
por tal situação consistiu-se na criação dos números fracionários.
A organização do sistema numérico fracionário dos egípcios era
baseada no conceito unitário, de forma que a maioria das frações
apresentava o seu numerador constituído pelo numeral 1 (um) –
representado por um sinal de forma oval e alongada. Tais frações eram
denominadas frações unitárias ou egípcias. Assim: 1/8 correspondia a um
símbolo, 1/20 correspondia a outro símbolo. Todavia, duas frações podiam
ser apontadas como exceção a tal regra: 3/4 e 2/3, sendo que o último
era contemplado como fração geral, uma vez que era utilizada como base
para diversas operações matemáticas.
Muitas das frações que não apresentavam o numeral 1 no numerador eram
consideradas o resultado da soma entre as várias frações egípcias
(unitárias). Porém, é importante ressaltar que os sinais de adição e
subtração não eram utilizados nestas operações matemáticas, visto que
ainda não tinham sidos criados.
Os antigos egípcios usavam um sistema de frações baseado em caracteres
distintos, tipo 1/2 era um símbolo, 3/4 era outro, etc., mas tinham
alguma regra geral. Em particular, as frações do tipo 1/2n
(que seriam tipo 1/2, 1/4, 1/8, 1/16, 1/32...) tinham símbolos
especiais, surgindo da associação desses símbolos, do 1/2 até o 1/64 é o
olho de Horus. Tem a ver com a série infinita 1/2 + 1/4 + 1/8 + 1/16 +
1/32 ... = 1. Não se sabe se eles achavam que terminava no 1/64 porque
não conseguiam diferenciar pedaços de coisa menores que isso, mas a
idéia seria que todos juntos formariam a unidade. Cada fração
representaria um sentido, tipo visão, olfato, paladar, tato, audição, e o
sexto sentido, que seria o pensamento. A Figura 4 mostra, no olho de
Horus, quais são os símbolos de cada fração:
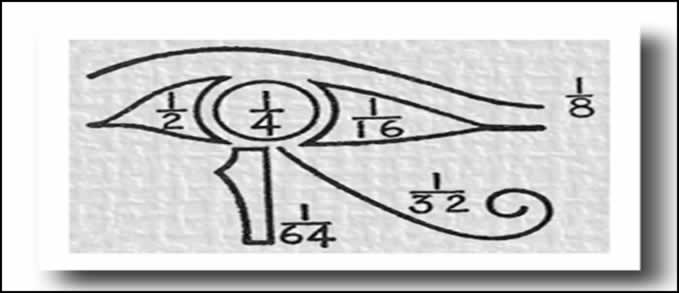
Figura 4:Olho de Horus.
Fonte: Bakos(2005, p. 60).
Onde:
- 1/2 representa o olfato;
- 1/4 representa a visão;
- 1/8 representa o pensamento, que seria a sobrancelha;
- 1/16 representa a audição;
- 1/32 representa o paladar, uma lingüinha bem comprida;
- 1/64 representa o tato, que seriam as duas perninhas em contato com o mundo embaixo.
Conforme Zamboni (2001), é válido apontar a existência de grande
variação na representação do sistema fracionário segundo a sociedade e a
época histórica. Assim, ao passo que os egípcios utilizavam frações
unitárias na maioria das vezes, os babilônicos e os Sumérios, já por
volta da segunda metade do terceiro milênio, faziam uso de frações cujo
denominador era 60. Era um sistema sexagesimal, onde os números menores
que 60 eram representados por um sistema de base 10 e os números maiores
ou iguais a 60 eram designados pelo mesmo principio com a base 60. Esse
sistema tinha base no princípio proporcional.
É provável que o uso do número 60 pelos babilônios se deve ao fato que
é um número menor do que 100 com maior quantidade de divisores
inteiros, os romanos, por sua vez, usavam constantemente frações com
denominador 12. Já os romanos usavam o número 12 por ser um número que
embora pequeno, possui um número expressivo de divisores inteiros.
De acordo com Zamboni (2001), com Grande parte do conhecimento
matemático vigente na Antiguidade foi resgatado pelo achado de inúmeros
registros feitos em papiros, transformando-os em valiosas fontes
históricas. Dois desses importantes documentos encontrados são o Papyrus Rhind e o Papyrus de Moscou,
que tratavam da resolução de diversos problemas matemáticos de caráter
cotidiano (a armazenagem do trigo, o preço do pão, a alimentação do
gado), e outros conteúdos de natureza fracionária.
Acredita-se, que tais documentos apresentavam funções meramente
pedagógicas, sendo destinado ao ensino de funcionários do estado egípcio
e dos escribas. Assim, as frações, desde o tempo dos egípcios auxiliam
de modo significativo ao longo da história o homem no sentido de
facilitar seu processo de compreensão do mundo que o rodeia e de suas
próprias ações.
4. O ENSINO DOS NÚMEROS FRACIONÁRIOS NO ENSINO FUNDAMENTAL
4.1 AIdéia de Número Fracionário
A idéia de número fracionário surge da necessidade de se considerar
uma ou mais partes de um objeto (o todo). De maneira geral, é
representado na forma a/b, onde; bé o denominador que
indica partes iguais que se divide a unidade e é o numerador que indica
quantas dessas partes foram consideradas, devendo o denominador ser
sempre diferente de zero.
O significado do vocábulo fração vem do latim fragere que
significa “quebrar”. Os termos “denominador” e “numerador” possuem
origem latina e significam respectivamente, dar nomes e contar. Ao
realizar a leitura de uma fração, deve-se iniciar pelo numerador e a
seguir partir para o termo referente ao denominador.
A barra foi introduzida pelos árabes no século XIII, advindo do
esquema numerador-denominador, utilizado na Índia. Ela foi utilizada
pela primeira vez pelo matemático italiano Fibonacci. O Símbolo para
indicar uma porcentagem (%), evoluiu a partir de uma figura semelhante
encontrada em um manuscrito italiano anônimo de 1425 que trazia diversas
frações de denominador 100. A primeira vírgula surgiu num texto
contábil em 1492, na Itália, indicando a divisão de um número por uma
potência de 10. Um século depois, passou a ser usada para separar a
parte inteira da parte decimal de um número, como, por exemplo, em 0,5. O
traço diagonal surgiu por uma necessidade da impressa, pois ao publicar
uma fração era preciso montar tipos em três andares.
De acordo com Lezzi (2001), existem diferentes tipos de fração:
- Frações própriassão aquelas cujo numerador é menor que o denominador e diferente de zero, exemplo 3/5; essas frações são próprias de um único inteiro;
- Frações imprópriassão aquelas cujo numerador é maior que o denominador, mas não é múltiplo do mesmo, exemplo 5/2; essas frações não são próprias de um único inteiro;
- Frações aparentessão aquelas cujo numerador é múltiplo do denominador; ela tem apenas aparência de fração, exemplo 9/3;
- Frações equivalentessão aquelas que representam a mesma parte do todo; são escritas de formas diferentes, mas que representam a mesma quantidade. Exemplo: Um chocolate foi repartido em 6 partes iguais, logo cada parte representa 1/6 do chocolate todo. Se pegarmos 3 dessas partes estaremos com 3/6 do chocolate todo, mas isso representa também a metade do chocolate, 1/2. Dizemos então que 1/2 e 3/6 são frações equivalentes;
- Frações decimaissão aquelas em que os denominadores são múltiplos de 10. Exemplo: 1/20, 2/20.
Podemos realizar as quatro operações básicas da matemática utilizando
frações em suas mais variadas formas de apresentação, bem como podemos
trabalhar com potenciação e extração de raiz quadrada, as frações
algébricas (incluindo as operações básicas), dentre outras operações
conhecidas no meio matemático. Para realizar estas operações faz-se
necessário que o professor utilize muitos exemplos práticos e faça
atividades com situações que despertem a curiosidade do aluno em
encontrar a resposta. Alguns desses exemplos práticos podem ser
realizados através de divisões com papel colorido, áreas de sala de aula
ou outros ambientes da escola.
Para uma criança não é tão fácil entender que a fração é um modo de
expressar uma quantidade a partir de um valor que é dividido por um
determinado número em partes iguais entre si. E o ensino da Matemática
muitas vezes está apenas ligado à transmissão de passos e regras. Os
alunos precisam entender, como os egípcios, que os números naturais são
insuficientes para resolver determinados problemas. Não conseguem
exprimir a medida de uma grandeza ou resultado de uma divisão. Para
isto, se utiliza os números racionais.
A utilização da história da Matemática pode ajudar a formar definições
a respeito do estudo das frações. Um texto sobre a problemática da
divisão das terras do Nilo é uma das formas de introduzir o conteúdo. É
uma situação problema que leva o educando a percebe a importância de um
numero que representasse uma quantidade inferior a um inteiro, ou seja, o
número fracionário.
Conforme os PCNs (BRASIL, 1997) a aprendizagem dos números racionais
supõe rupturas com idéias construídas acerca dos números naturais, e,
portanto, demanda tempo e uma abordagem adequada.
O aluno precisa compreender que a fração é uma linguagem para
representar números ou relações entre números e que ele tenha interesse
em decodificá-la e relacionar o seu significado ao contexto real.
Conforme os PCNs (2007), é indispensável, ao fazer um estudo dos
números fracionários, reconhecer e tomar conhecimento da faixa etária do
aluno e, sobretudo, do nível de escolaridade a quem se pretende ensinar
tal conteúdo. De acordo com os PCNs de Matemática, é no segundo ciclo
(3ase 4asséries do Ensino
Fundamental de 8 anos), que são apresentadas aos alunos
situações-problema cujas soluções não se encontram no campo dos números
naturais, possibilitando, assim, que eles se aproximem da noção de
número racional, pela compreensão de alguns de seus significados
(parte-todo, razão e quociente) e de suas representações, fracionária e
decimal.
As orientações didáticas recomendam a exploração dos diferentes
significados das frações em situações problemas: parte-todo, quociente e
razão. A prática mais comum para explorar o conceito de fração é a que
recorre a saturações em que está implícita a relação parte-todo; é o
caos das tradicionais divisões de um chocolate ou uma pizza em partes
iguais. A fração indica a relação que existe entre um número de partes
consideradas e o total de partes em que o inteiro foi dividido.
Fração com significado parte todo é a partição de um objeto qualquer
em n partes, isto é, um todo dividido em partes iguais e que cada parte
poderá ser representada como 1/n, chagando-se a uma resposta correta.
Esta é uma prática comum para explorar o conceito de fração, é o caso
das tradicionais divisões de um chocolate ou de uma pizza em partes
iguais. A fração indica a relação que existe entre um número de partes
consideradas e o total de partes em que o inteiro foi dividido.
- Fração com significado quociente está presente em situações de partição. Exemplo: duas pizzas foram divididas igualmente para 3 pessoas. Quanto recebeu cada uma?
O significado das frações como quociente baseia-se na divisão de um número natural por outro: a:b = a/b.
Essa definição se diferencia da anterior (parte-todo), porque dividir
um chocolate em 3 partes e comer 2 dessas partes é uma situação
diferente daquela em que é preciso dividir 2 chocolates para 3 pessoas,
mesmo que nos dois casos o resultado seja representado pela mesma
notação: 2/3 (BRASIL, 1997).
- Na terceira situação, onde a fração é interpretada como razão, essa fração é usada como uma espécie de índice comparativo entre duas quantidades de uma grandeza.
A fração é usada como razão quando temos situações do tipo: 2 de cada 3 habitantes de uma cidade são imigrantes.
Antes de se entender o sentido matemático de uma fração, se deve
compreender o que seja um inteiro, através da manipulação de materiais
concretos, como peças geométricas, como tangram, blocos fracionários que
induzam a montar, desmontar e relacionar as partes com o todo. Ficar
colorindo figuras dos livros didáticos pode não ajudar e se tornar perda
de tempo.
O conteúdo dos números fracionários e decimais não são esgotados
nessas séries, pois esse ciclo não constitui um marco de terminalidade
da aprendizagem desses conteúdos, o que significa que o trabalho com
números naturais e racionais, operações, medidas, espaço e forma e o
tratamento da informação deverá ter continuidade, para que o aluno
alcance novos patamares de conhecimento (BRASIL,1997, p. 59).
Muitas vezes, ao raciocinar sobre números racionais como se fossem
naturais, os alunos acabam enfrentando obstáculos como o fato de que o
número racional pode ser representado por diferentes (e infinitas)
escritas fracionárias; a comparação entre racionais, onde 1/3 < 1/2,
pode lhes parecer contraditório aos naturais 3 > 2; a indicação de
grandeza não obedece aos mesmos critérios dos naturais (5.230 > 25) e
2,3 e 2,125; ao se multiplicar um número natural por outro natural
diferente de 0 ou 1 se encontraria um número maior que ambos, com os
fracionários, ao se multiplicar 10 por 1/2 se surpreenderam ao verificar
que o resultado é menor que 10 (BRASIL, 1997).
Se a seqüência dos números naturais permite falar em sucessor e
antecessor, para os racionais, isso não faz sentido, uma vez que entre
dois números racionais quaisquer é sempre possível encontrar outro
racional; assim, o aluno deverá perceber que entre 0,8 e 0,9 estão
números como 0,81, 0,815 ou 0,87 (BRASIL, 1997, p. 68).
Os números decimais têm origem nas frações decimais. Por exemplos
temos a fração 1/2 que equivale à fração 5/10 que equivale ao número
decimal 0,5. Em 1585 o engenheiro e matemático holandês Stevin, ensinou
um método para efetuar todas as operações por meio de inteiros, em o uso
de frações, onde escrevia os números naturais ordenados em cima de cada
algarismo de numerador indicando a posição ocupada pela vírgula no
numeral decimal (BRASIL, 1997).
Vejamos a notação adaptada pelo grande matemático escocês John Napier:
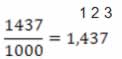
Entre os conteúdos conceituais e procedimentais contidos no Currículo
Nacional de Matemática para o segundo ciclo estão presentes: os Números
Naturais; Sistema de Numeração Decimal e Números Racionais; Operações
com Números Naturais e Racionais; Espaço e Forma; Grandezas e Medidas; e
Tratamento da Informação. No terceiro ciclo do Ensino fundamental a
sugestão é de que se introduza o significado de operador multiplicativo.
O que mais importa estudar no presente trabalho, no entanto, é o que
diz respeito aos números racionais, em específico os números
fracionários. Portanto, vamos nos ater mais a eles.
4.2 O Ensino dos Números Fracionários no 2º Ciclo do Ensino Fundamental (5ª e 6ª série)
Espera-se que no segundo ciclo do Ensino Fundamental, o aluno,
conforme os PCNs (BRASIL, 1997), reconheça os números naturais e
racionais no contexto diários, compreenda e utilize as regras do sistema
de numeração decimal, para leitura, escrita, comparação e ordenação de
números naturais de qualquer ordem de grandeza; formule hipóteses sobre a
grandeza numérica, pela observação da posição dos algarismos na
representação decimal de um número racional; leia e represente os
números racionais na forma decimal; compare e ordene os números
racionaís na forma decimal; localize na reta numérica, de números
racionais na forma decimal; leia, escreva, compare e ordene as
representações fracionárias de uso freqüente; reconheça que os números
racionais admitem diferentes (infinitas) representações na forma
fracionária; identifique e produza frações equivalentes, pela observação
de representações gráficas e de regularidades nas escritas numéricas;
explore os diferentes significados das frações em situações-problema:
parte todo, quociente e razão; observe que os números naturais podem ser
expressos na forma fracionária; relacione as representações
fracionárias com a decimal de um mesmo número racional; e reconheça o
uso da porcentagem no contexto diário.
4.3 As Falhas no Ensino de Frações Hoje
Analisando alguns autores de livros do 6º ano (antiga 5ª
série), foi possível verificar que quando é apresentado o conteúdo do
tipo: multiplicar frações por números naturais ou inteiros ocorrem
aplicações errôneas, mesmo que existam algumas sobreposições. São
artifícios usados como afirmações do tipo: "Multiplicar um número
inteiro por uma fração com o denominador um", notasse, no entanto, que o
aluno esta aprendendo a tomar uma fração (unitária) de um número
inteiro e somente pode tomar a fração se o resultado também for um
número inteiro - na realidade, um caso raro, todavia, um artifício comum
na ficção curricular. Em nenhum lugar do texto é mencionado que estamos
lidando com um caso muito particular de um problema geral. Em outra
abordagem enfoca-se o seguinte conteúdo "escrever frações como
porcentagem" simplesmente se referem a frações com denominador cem.
Outro exemplo da ausência do conhecimento amplo sobre o assunto é quando
apresenta a expressão matemática: escrever "1/3 x 12" abaixo de "1/3 de
12" e deste modo afirmar que estamos aprendendo a multiplicar frações.
Não existem explicações de porque nós chamamos multiplicação o processo
de achar 1/3 de 12. Um outro texto adota um artifício diferente, porém
ainda mais enganador - tendo demonstrado que 12 x 1/3 = 4 por adições
repetitivas na linha seguinte da que 1/3 x12 = 4 sem nenhuma explicação
(BRASIL, 1997).
A inviabilidade complementar também é encontrada freqüentemente. O
texto demonstra, recolocando pedaços de retângulo, que 1/2 X 1/3 = 1/6.
Então escreve que 1/2 X 1/3 = (1x1) (2x3) = 1/6, e conclui que em
multiplicação de frações basta multiplicar os numeradores e os
denominadores. É razoável duvidar que o aluno, observando que 1/2 x1/3
=1/6, percebesse estar multiplicando 1x1 para obter 1 (BRASIL, 1997).
Um exemplo final de inviabilidade precisa e, deveria ser suficiente,
para somar duas frações: dizem-nos que devemos achar o menor denominador
comum (uma frase equivocada, uma vez que nós somente temos que achar o
menor denominador comum quando as frações envolvidas não têm um
denominador comum); Isto é normalmente apresentado em três estágios:
Primeiro, se as frações têm o mesmo denominador este é o menor
denominador comum; Se um denominador é múltiplo do outro, utilize-o como
menor denominador comum. E o terceiro estágio ainda é menos explicito:
muitos textos dão imediatamente exemplos como 2/7 + 5/12 e dizem que
"use 7 x 12". Outros dão exemplos com 34 + 56 e dizem "tentem 12".
Contudo, não há menção de nenhum processo sistemático, nenhuma sugestão
mesmo para dizer quando você deve multiplicar os dois denominadores
(BRASIL, 1997). O aluno é levado a acreditar que lhe foi ensinado um
procedimento e que o aprendeu, mais isso não é verdade.
4.4 Sugestões Metodológicas para um Bom Ensino sobre Frações
Devemos vivenciar situações de contextualizações, onde apareçam o
conceito, parte-todo, quociente, comparações, equivalências e as
operações. Após fazer análise, observações de métodos aplicados no
ensino das frações, em várias edições recentes, mesmo que estes métodos
não possam ser todos descartáveis, vem a seguinte indagação: “será
possível no ensino de frações, desenvolver novas metodologias e
aplicações que visem uma melhor compreensão destas?”.
Sim, percebermos que normalmente as crianças têm contato com medidas e
valores monetários, nos quais aparecem o décimo e o centésimo, no
entanto, o nosso ambiente não coloca para elas, problemas significativos
envolvendo números fracionários. Não compramos 3/4 de dúzias de
bananas, nem 5/8 de pizza. O vocabulário mais comum em relação ao tema é
o meio ou a quarta parte (de certa quantidade), ½ ou ¼ de uma hora.
Os materiais concretos podem ter formas geométricas, tiras de papel em
tamanhos e cores diferentes, botões, palitos, tampinhas, grãos, fita
métrica e balança.
Há diversas metodologias que podem ser aproveitadas para o ensino de
frações. Algumas delas consistem na utilização de materiais concretos,
livros didáticos, jogos ou suporte da informática e multimídia, porém
todas devem levar em consideração o contexto e o uso cotidiano do aluno.
Percebemos que atualmente as escolas, públicas em geral, como também
algumas particulares vêm a cada dia exigindo menos dos alunos em relação
aos cálculos com frações nas situações do cotidiano.
Outra sugestão com relação às dificuldades metodológicas é a aplicação
do conteúdo de frações na qual chagamos a uma conclusão: é que quando
falamos em adição de frações com denominadores diferentes, geralmente,
recorremos em sala de aula a uma regra tradicional que consiste em
determinar o mínimo múltiplo comum (mmc) dos denominadores, sendo que,
depois, é necessário fazer algumas operações com o intuito de encontrar
frações equivalentes as duas frações dadas com o mesmo denominador.
Todo esse processo causa enorme desânimo em boa parte dos alunos, já
que a operação “divisão” é para muitos um entrave no seu aprendizado.
Contudo, graças às nossa busca por novas técnicas, conseguimos encontrar
algumas muito interessantes e entre elas destacamos a seguinte, que por
ser de melhor compreensão, a operação “multiplicação” torna essa
técnica mais agradável e simples. Vejamos a situação abaixo, na qual se
pede que se determine a soma das frações que se seguem:
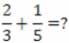
1º) Deve-se encontrar quais frações equivalentes às respectivas
frações dadas acima que possuam os mesmos denominadores. Então, tem-se:
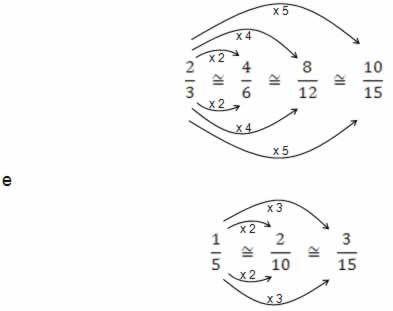
2º) Em seguida, substitui-se as frações dadas pelas suas respectivas equivalências e efetua-se a operação. Assim, tem-se:
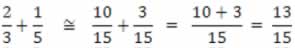
Nosso objetivo é tornar possível, o uso dos números fracionários nas
operações básicas: adição, subtração, multiplicação e divisão, como
também suas aplicações nas diversas áreas do setor profissionalizante,
como por exemplo: marcenaria (fabricação de peças de móveis); tornearia e
mecânica (montagem de peças para máquinas, automóveis e outros);
comércio (tecidos, alimentos, hortifrutigranjeiros), entre outros.
E ainda mais, por meio de situações do cotidiano, onde ocorrem
inúmeras situações nas quais se empregam frações, como por exemplo, nas
eleições, onde vence o candidato que obtiver ½ (metade) do total de
votos mais um no primeiro turno, ou a maioria simples no segundo; em
mapas e plantas com o uso de escalas; em razões e proporções empregadas
na música, na medicina, na física, na culinária (receitas de tortas,
salgados), entre outras aplicações.
4.5 Reflexões sobre o Ensino de Frações no Currículo de Matemática
Ainda existem muitos mitos e equívocos a respeito do currículo de
matemática e sua implementação. Um dos mais preocupantes é o de que um
tópico específico ou campo conceitual é exclusividade de uma determinada
série. Há muitas décadas que o tema frações com todo seu acervo de
conceitos e procedimentos subjacentes (frações próprias, equivalentes,
ordenação, aplicações e operações) podem e devem ser "ensinados" na 5a
série como um pacote. Esta “tradição” é um grande erro, principalmente
porque obriga o professor a ensinar muito conteúdo em pouco tempo e não
deixa o aluno assimilar de acordo com suas necessidades o que está
aprendendo. Será que os alunos realmente aprendem? E o que aprendem?
Muitas vezes, o aluno só aprende o que interessa para a prova,
procurando obter uma nota. É por isso que, em geral, não transferem seus
conhecimentos sobre frações para situações em que não foram ensinados e
se esquecem do que aprenderam quando passam para as séries seguintes. O
professor, por sua vez, deveria repensar sua forma de ensinar frações.
Será que não está na hora de abrir mão dos velhos recursos de partir
pizzas e barras de chocolate? Centenas de estudos sobre aprendizagem de
frações, números racionais e atividades de proporcionalidade que mostram
que há diferentes e diversas idéias em torno de um código 3/4. Levar os
alunos a descobrir a regra de divisão de frações seria um novo recomeço
no ensino das frações. Sabe-se, baseado em investigações, que as
crianças têm concepções diversas sobre frações e a passagem de uma idéia
para outra como da relação parte-todo para a fração como número ou
razão não é simples e leva tempo.
Investigações sérias mostram que a formação do pensamento proporcional
é longa, estendendo-se dos 9/10 anos até os 14/15 anos. Não é de se
estranhar, portanto, que os alunos tenham dificuldades, e que certos
conceitos e procedimentos têm permanência curta, resistindo quando
muito, do dia do "ponto ensinado" ao dia da prova. Esses mesmos estudos
sugerem que o ensino de frações deve ser gradativo, que deveríamos dosar
o ensino das operações de modo que elas possam ser realmente
conceituadas e incorporadas às estruturas de pensamento dos alunos.
É necessário que os alunos pensem, elaborem hipóteses, apresentem
respostas e repensem até se certificarem da solução encontrada.
5. AS FRAÇÕES NA MATEMÁTICA HOJE
Conforme os PCNs (BRASIL, 1997), os conteúdos sobre frações indicados
para trabalhar o segundo ciclo são: o reconhecimento dos números
racionais no contexto diário; leitura, escrita, comparação e ordenação
de representação fracionária de uso freqüente; reconhecer que números
racionais admitem diferentes representações na forma fracionária, dentre
outros.
A distribuição do conteúdo envolve atividades de conceitualização e uso das frações ao longo das 4 séries (5a a 8a). De modo que os alunos possam ser introduzidos ao estudo das frações na 5a série (6o ano) e, caso já tenham estudado frações na 4a série, o trabalho na 5a
pode funcionar como revisão, reforço e introdução de novas situações,
com ênfase no conceito de fração equivalente e nas operações aditivas
(adição e subtração). A equivalência é utilizada para introduzir a forma
decimal e para em seguida introduzir ou explorar as porcentagens.
Na 6a série (7o ano) é feita uma
revisão com problemas e situações novas que vão ajudar na problematizar
de forma que os alunos explorem as operações de natureza multiplicativa
(multiplicação e divisão). Ainda no 7o ano a notação fracionária é utilizada nas situações usualmente intituladas de "razões e proporções".
Uma retomada é feita na 7a série (8o ano)
onde, numa perspectiva algébrica a fração é conceituada como número
racional, formando o conjunto Q dos racionais, que surge como o primeiro
conjunto denso que os alunos têm contato. A densidade é uma importante
propriedade de conjuntos numéricos. O conjunto Q é dito denso porque
dados quaisquer racionais x1 e x2 existe sempre um outro número racional
entre eles. Esta propriedade pode ser provada quando se propõe aos
alunos que achem a média aritmética de dois racionais quaisquer. Uma
importante utilização dos racionais é feita nesta série com a introdução
às probabilidades. Diferentemente dos países desenvolvidos, no Brasil o
estudo das probabilidades era exclusivo do currículo ensino médio.
Na 8a série (9o ano) os alunos são
convidados a fazer um balanço formal de seus conhecimentos numéricos
colocando os conjuntos dos vários tipos de números, que já dominam, em
relação uns com os outros de modo a descobrir novas propriedades,
estender definições, dentre outros. No final do 9º Ano, quando estão
estudando matemática comercial e financeira utilizam os números
racionais na forma fracionária ou decimal como operadores: taxas,
fatores de aumento ou decréscimo.
Devemos introduzir explicitamente os números racionais (nós nos referimos aqui aos racionais positivos;
o conjunto todo dos racionais aparecerá, é claro, uma vez que os
números negativos sejam introduzidos) – e que não haveria dificuldades
em fazê-lo.
Deveríamos apresentar a multiplicação como uma operação básica com números racionais. Isto é matematicamente
correto já que os números racionais surgem do desejo, ou necessidade,
de inverter a multiplicação e é correto na prática porque é mais fácil
encontrar aplicações da multiplicação de frações. A divisão por números
racionais não apresenta nenhum problema real, matematicamente falando,
mas é mais difícil encontrar aplicações convenientes. Há questões do
tipo "quanto?" que pedem divisões de frações, mas nas quais a resposta é
obtida arredondando-se o quociente para cima ou para baixo, para um
número inteiro. Há outras questões (por exemplo, o preço de um imposto
ou de uma redução percentual) que levam a divisão de decimais por
frações. Desta maneira, nós devemos admitir honestamente que a divisão
exata de números racionais por números racionais não é uma ferramenta
prática muito importante, certamente não se comporta como a
multiplicação.
Os melhores exemplos vêm da teoria elementar de probabilidade, onde a
probabilidade de uma disjunção completa de dois eventos (mutuamente
exclusivos) é a soma das probabilidades dos dois eventos. Deve ser
notado, contudo, que nesta aplicação as duas probabilidades tendem
naturalmente a ser representadas por frações com o mesmo denominador.
Deste modo, se eu atiro dois dados e somo os números das faces de cima, a
probabilidade de obter 4 é 3/36 e a probabilidade de obter 8 é 5/36 de
modo que a probabilidade de obter 4 ou 8 é 8/36. Seria perverso
expressar a primeira probabilidade como 1/12 e assim complicar a tarefa
de somar as frações-simplicidade não reside na fração, mas no processo
aritmético no qual se usa a fração. Mesmo apresentar a resposta como 2/9
é desnecessário e talvez irracional, se, por exemplo, quisermos
comparar a probabilidade de obter 4 ou 8 com a probabilidade de obter 7.
A subtração de frações é de muito menos importância na prática do que a
adição de frações e isto novamente deveria ser honestamente admitido.
Há aplicações naturais para a subtração de frações simples, mas a
principal justificativa para se gastar tempo com este tópico é que isto é
matematicamente importante. Essa justificativa é válida – mas não
justifica a ênfase demasiada neste tópico, nem o monótono trabalho
realizado para inculcar confiança na execução do que não passa de um
algoritmo banal.
Há dois pontos adicionais a mencionar nesta questão. Primeiro, a
intuição deveria desempenhar um papel muito maior na aritmética de
frações do que na álgebra de funções racionais. Não se deseja que um
aluno calcule ½ + ½, ou mesmo ½ + ¾, com auxílio da regra para calcular
a/b + c/d. Desta maneira, nos casos mais importantes, o de algoritmo não
será usado. Segundo, há uma diferença importante entre os dois tópicos.
Um aspecto muito importante da álgebra de funções racionais é a
expansão em frações parciais. O processo análogo para números racionais é
muito menos importante, e nem sequer é único. Deste modo 1/6 = 2/3 - ½ =
½ -1/3. É claro, o momento oportuno par tratar esta questão, e par
considerar a razão par os diferentes comportamentos nos dois casos, é
quando se está estudando funções racionais.
6. CONSIDERAÇÕES FINAIS
Este estudo possibilitou conhecer a história das frações, compreender a
sua importância nas séries iniciais, evidenciando a necessidade de
rever a metodologia aplicada, como também de promoção de mudanças que
venham a facilitar a aprendizagem deste conteúdo de tão grande
importância e utilização histórica. E, mesmo com o uso da tecnologia das
calculadoras e dos computadores de última geração, para se obter
resultados de forma rápida e precisa e também para resolver problemas
considerados difíceis, o homem tem a necessidade do conhecimento
matemático. Assim, faz-se necessário dinamizar o processo
ensino-aprendizagem das frações, no sentido de despertar no docente e no
discente os aspectos da aplicabilidade desse conteúdo na sala de aula e
no próprio dia-a-dia, levando-os a despertar o gosto pelo estudo e a
pesquisa. Não adianta dizer ao discente que esse ou aquele assunto é
importante porque vai cair na prova ou porque está no programa. Ou então
continuar usando os mesmos exemplos para todas as séries para
exemplificar frações como é o que acontece com a barra de chocolate e a
pizza.
Em vários momentos da vida é necessário analisar situações, refletir
sobre assuntos diversos, tomar decisões e argumentar para deixar claro
nosso ponto de vista. O que nos torna diferentes dos animais é a
capacidade de contagem, que permite que superemos as limitações de
nossos sentidos. A capacidade de associação tem grande importância na
resolução de problemas do cotidiano quando temos o saber matemático. O
docente deve pesquisar em diversas fontes o assunto que irá trabalhar em
sala de aula, ele deve planejar e aplicar metodologias que venham a
ajudar seus alunos de forma que todos tenham a capacidade de reconhecer a
aplicabilidade do que foi estudado, neste caso, as frações. Para isto, o
professor passa por um processo de formação pedagógico, intencional e
organizado, composto de várias fases.
Muitas vezes, é difícil para o aluno do Ensino Fundamental assimilar o
conceito de fração e alguns livros usam uma linguagem ainda mais
difícil ou partem diretamente para o cálculo sem que haja uma introdução
do assunto ou uma fundamentação que desperte o interesse em aprender
tal conteúdo.
7. REFERÊNCIAS BIBLIOGRÁFICAS
BAKOS, Margaret Marchiori (org.). O Imperador na Terra dos Faraós. Revista Nossa História, São Paulo, jan. 2005, n. 15, v. 2.
BOYER, Carl Benjamim. História da matemática. Tradução: Elza F. Gomide. São Paulo: Ed. Edgard, 1996.
BRASIL. Ministério da Educação. Parâmetros Curriculares Nacionais para o Ensino Fundamental. 1 a 4 séries, Brasília. SEF, 1997.
_______. Ministério da Educação. Parâmetros Curriculares Nacionais para o Ensino Fundamental. 5 a 8 séries, Brasília. SEF, 1998.
GIL, A. C. Métodos e técnicas de pesquisa social. 5. ed. São Paulo: Atlas, 1999.
IEZZI, Gelson. Matemática e realidade – 5ª Série do Ensino Fundamental. Nova Edição. São Paulo: Atual Editora, 2001.
KILPATRICK, J. (1994). Investigación em Educación Matemática: Su Historia y Alguns Temas de Actualidad. In: KILPATRICK, Rico. Educación matemática. México; Grupo Editorial Iberoamerica, 1992.
LAMPERT, M.; BALL, D. L. Teaching, multimedia, and mathematics. New York: Teachers, College Press, 1998.
LIBÂNEO, José Carlos. Didática. São Paulo: Cortez, 1994. (Coleção Magistério. 2º grau. Série de formação do professor).
MARROU, H. I. História da educação na antiguidade. São Paulo: Epul, 1975.
MATSUBARA, Roberto. Big Mat – Matemática: história, evolução, conscientização. 5. série. 2. ed. São Paulo: IBEP, 2002.
MIORIM, M. A. História da educação matemática. São Paulo: Atual, 1998.
PILETTI, Claudino. Didática geral. 23. ed. São Paulo: Editora Ática: 2003.
RÚDIO, Franz Victor – Introdução ao Projeto de Pesquisa Cientifica. Petrópolis – Rj –- Ed. Vozes. 1980. 124 p.
SCHUBRING, G. O primeiro movimento internacional de reforma Curricular em Matemática e o papel da Alemanha. Vol. 7, São Paulo: Ed. Zetetiké, 1999.
TOLEDO, M. Didática de matemática: como dois e dois: a construção da Matemática. São Paulo: FTD, 1997.
ZAMBONI, Sílvio. A pesquisa em arte: um paralelo entre arte e ciência. 2. ed. Campinas, SP: Autores Associados, 2001.

Nenhum comentário:
Postar um comentário