sábado, 22 de dezembro de 2012

Identidade Trigonométrica

 Uma identidade trigonométrica é uma equação envolvendo funções trigonométricas e que é verdadeira para todos os valores das variáveis envolvidas. Estas identidades são úteis sempre que expressões envolvendo funções trigonométricas devam ser simplificadas. Uma importante aplicação é a integração de funções não-trigonométricas: um truque comum envolve primeiro usar a integração por substituição com uma função trigonométrica e então simplificar a integral resultante com uma identidade trigonométrica.

Ângulos
Esse artigo utiliza letras gregas tais como alfa (α), beta (β), theta (θ) e Phi (φ) para representar ângulos. Várias unidades de ângulo são largamente utilizadas, incluindo graus, radianos e grados:
1 volta completa  = 360 graus = 2\pi radianos  =  400 grados.
A tabela a seguir mostra as conversões para alguns ângulos comuns:
Graus 30° 60° 120° 150° 210° 240° 300° 330°
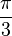Radianos \frac\pi6\! \frac\pi3\! \frac{2\pi}3\! \frac{5\pi}6\! \frac{7\pi}6\! \frac{4\pi}3\! \frac{5\pi}3\! \frac{11\pi}6\!
Grados 33⅓ grados 66⅔ grados 133⅓ grados 166⅔ grados 233⅓ grados 266⅔ grados 333⅓ grados 366⅔ grados

Graus 45° 90° 135° 180° 225° 270° 315° 360°
Radianos \frac\pi4\! \frac\pi2\! \frac{3\pi}4\! \pi\! \frac{5\pi}4\! \frac{3\pi}2\! \frac{7\pi}4\! 2\pi\!
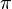Grados 50 grados 100 grados 150 grados 200 grados 250 grados 300 grados 350 grados 400 grados


Funções trigonométricas

As funções trigonométricas básicas são o seno e o cosseno de um ângulo. Essas são abreviadas por sen(θ) e cos(θ), respectivamente, onde θ é o ângulo. Todavia as parênteses podem ser omitidas, como por exemplo sen θ and cos θ.

A função tangente (tg ou tan) de um ângulo é a razão do seno e o cosseno de um mesmo ângulo:
\tan\theta = \frac{\sen\theta}{\cos\theta}.
Finalmente, as funções trigonométricas de razão recíproca secante (sec), cossecante (csc) e cotangente (ctg), das funções cosseno, seno e tangente:
    
 \tan\theta = \frac {\operatorname{sen}\theta}{\cos\theta}\,\!
\cot\theta = \frac {1}{\tan\theta}\,\!
\sec\theta = \frac {1}{\cos\theta}\,\!

\csc\theta = \frac {1}{\operatorname{sen}\theta}\,\! 
As funções inversas trigonométricas são funções inversas parciais. Por exemplo a função inversa de seno, (sen−1) ou arco seno (arcsen), deve satisfazer:
\sen(\operatorname{arcsen}) = x\quad\text{para} \quad |x| \leq 1
e
\operatorname{arcsen}(\sen x) = x\quad\text{para} \quad |x| \leq \pi/2
Função sen cos tan sec csc cot
Inversa arcsen arccos arctan arcsec arccsc arccot



A relação básica entre seno e cosseno é a identidade trigonométrica fundamental:
\cos^2\theta + \sen^2\theta = 1\!
onde cos2 θ é igual (cos(θ))2 e sen2 θ é igual (sen(θ))2.
Isto pode ser deduzido através do Teorema de Pitágoras, vindo da equação x2 + y2 = 1 para um círculo unitário. Essa equação pode ser resolvida tanto com seno quanto com cosseno:
\sen\theta = \pm \sqrt{1-\cos^2\theta} \quad \text{e} \quad \cos\theta = \pm \sqrt{1 - \sen^2\theta}. \,     

Postado por às
Marcadores:

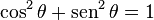
Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)