Função Afim ou Polinomial do 1º Grau

Para a confecção de apostilas uma gráfica cobra um valor de R$ 5,00 referentes ao custo da capa, contra-capa e da encadernação, mais um valor de R$ 0,50 para cada página da apostila.

Repare que há uma relação de dependência entre duas grandezas, o número de páginas da apostila e o seu custo total.

Para cada número de páginas existe um valor único para a apostila. Estamos então diante de uma função que pode ser definida como:

Ou, se trabalharmos com números fracionários, por:

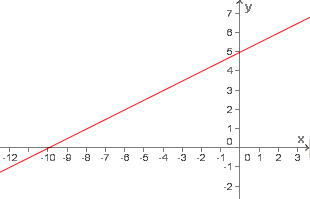Graficamente temos a seguinte representação da função no plano cartesiano:
Toda função na forma , com ( e ) é denominada função afim, ou função polinomial do 1° grau. Como sabemos, o polinômio ax + b é um polinômio do primeiro grau na variável x.
Como podemos observar o gráfico desta função é formado por uma reta. Toda função afim é representada no plano cartesiano por uma reta não paralela ao eixo x, ou eixo das abscissas.
Normalmente f(x) é representado pela letra y, como no caso deste gráfico. Então a função também pode ser definida por:

Representação Gráfica de uma Função Afim

Para montarmos o gráfico de uma função polinomial do 1° grau basta conhecermos dois pares ordenados cujo primeiro elemento pertence ao domínio da função e o segundo pertence à sua imagem.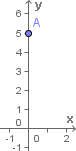
Para o primeiro par ordenado vamos escolher aquele onde x = 0. Substituindo x por 0 na regra de associação ou lei de formação da função, temos:

Então o nosso par ordenado será (0, 5) representado no gráfico ao lado pelo ponto A:
Voltando ao problema da apostila, o ponto (0, 5) do gráfico da função nos indica que caso a apostila não tenha nenhuma página, o seu custo será de R$ 5,00 referentes ao custo da capa, contra-capa e da encadernação apenas.
Para o outro par ordenado, arbitrariamente podemos escolher o ponto com abscissa igual a 4 e realizarmos os cálculos como no caso do primeiro ponto, agora trocando x por 4:

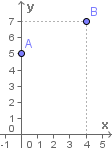
Tal ponto pode ser observado neste outro gráfico, representado pelo ponto B:
O ponto (4, 7) do gráfico da função nos aponta que o custo de uma apostila com 4 páginas é de R$ 7,00.
Como sabemos que o gráfico de uma função polinomial do 1° grau é uma reta, basta traçarmos uma reta unindo tais pontos, como podemos ver no gráfico abaixo:


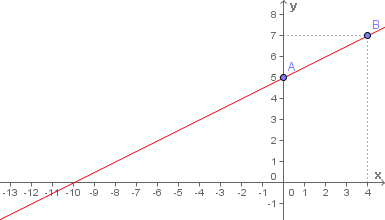
Observe que obtivemos o mesmo gráfico do início das explicações deste tópico.
Neste exemplo partimos da lei de formação da função, escolhemos arbitrariamente dois pontos conhecidos e a partir deles montamos o gráfico da função. Agora vamos obter a regra de associação da função a partir de quaisquer dois pontos conhecidos pertencentes à função.

Raiz da Função Afim

Observe no gráfico acima que a reta da função intercepta o eixo das abscissas no ponto (-10, 0).
Este valor de x = -10 que leva a y = 0 é denominado raiz da função ou zero da função.
Sendo a função, para encontramos a sua raiz basta substituirmos y por 0 e solucionarmos a equação do primeiro grau obtida:

Obtendo a Lei de Formação de uma Função Afim a partir de Dois Pontos da Reta

No gráfico acima vemos que o ponto (0, 5) pertence à função, então na sentença podemos trocar x por 0 e y por 5, quando então iremos obter que b = 5:

Novamente segundo o gráfico o ponto (-10, 0) também pertence à função e já que b = 5 temos:

Observe que substituímos y, x e b por 0, -10 e 5 respectivamente, obtendo a = ¹/₂.
Visto que a = ¹/₂ e b = 5, temos:

Portanto a função cujo gráfico passa pelos pontos (-10, 0) e (0, 5) é definida por:

Exatamente como havíamos visto no começo da matéria.
Vale ressaltar que chegaríamos à mesma definição da função, quaisquer que fossem os dois pontos distintos pertencentes a reta exemplo, que utilizássemos na realização dos cálculos.